『場の古典論』 第1章 相対性原理

1.相互作用の伝播速度

　読み物的な性格が強い節です。数式も出てきません。アインシュタインの相対性原理について書いてあって、大まかにまとめると
・相対性原理（あらゆる基準系で自然法則は同一）
・相互作用の伝播速度は有限で、ある最大値c≒3.0×10^8 m/sをもつ（光速度）
ということです。普通の相対論の本だとマイケルソン・モーレーの実験についてある程度説明するのですが、潔く「光の速度がその伝播方向にまったくよらないことを示した」と、たった2行程度で終わっていますね。何はともあれ、光の速度は一定で、そのため絶対的な時間というのが逆にあり得ないという話です。
　さて、ここからいよいよ「理論物理学教程シリーズ」の本領発揮ですよ…！

2.世界間隔

　いきなり「世界間隔」から始まるんですね(・_・;　他の本を見ると、まずはローレンツ変換を物理的な要請から導いて、その後にこの概念を導入するんですけどねぇ…ではローレンツ変換を本書ではどう定義してるんでしょうか？それは後々のお楽しみですね。
　まだローレンツ変換を知らない我々ですが、それでも世界間隔が慣性基準系によらないと示しています。5p.から6p.にかけての議論です。順序としては
・まず、ある慣性基準系で世界間隔が0ならばほかの慣性基準系でも0である（∵光速度不変の原理）
・上のことと、dsとds'が同じ次数であることからds^2=ads'^2という比例の関係であると示す
・aは二つの基準系の相対速度の大きさで決まるはずだが、3つの基準系を考えてみるとaは定数にならざるを得ない
・しかも、上で考えた関係式からa=1になる
　なんというか、「参りました」って感じですね。こういう、予想外のところからの攻撃にあふれているのが本書の魅力なんじゃないかなと思っています。初学の段階で読むより、一度ほかの教材で勉強してから改めてこの本を読んだ方が味わい深さも段違いだと思います。
　あとは「時間的」「空間的」に離れている、という状態についても述べられています。この本が採用している世界間隔の表式は
$ds^2 = c^2 dt^2 - dx^2 -dy^2 -dz^2$
と、-1が多いほうなので世界間隔が正だと時間的に、負だと空間的に離れています。意味合いとしては以下のようになります。
・時間的…基準系をうまく選ぶと2つの事象を同じ点で起きるようにはできるが、同時に起きるようにはできない。「過去」と「未来」が絶対的なものであり、因果関係が定義できる。
・空間的…基準系をうまく選ぶと2つの事象を同時に起こせるが、同じ点で起きるようにはできない。「過去」と「未来」が基準系によって変わるので、因果関係が定義できない。
詳しくは7p.の図なんかも参照してください。

3.固有時間

　次は「固有時間」というものについて説明しています。第1節で時間が慣性基準系によって変わってしまうということを学びました。これではすべての慣性基準系の時間を1つの時計で支配することができなくないわけですが、その代わりに各々の基準系に時計を与えて、自分たちで勝手に時間を管理させようというのが「固有時間」の発想です。アインシュタインはこのことについて「私は全宇宙に時計を置いた」と述べたそうです。

具体的には、次のようなことを考えます。
・系Sから見ると速さvで動いている物体がある
・系S'はその物体とともに動く慣性基準系である
このとき、第2節から系Sと系S'において世界間隔が等しいということが分かっているので
$c^{2}dt^{2}-dx^{2}-dy^{2}-dz^{2}=c^{2}dt'^{2}$
(dx'=dy'=dz'=0であるのは、系S'が物体とともに動く座標系だから)
${\frac {dx^{2}+dy^{2}+dz^{2}}{dt^{2}}}=v^{2}$
であることと、dt'が固有時間の微少変化dτに対応することから
$d\tau =dt{\sqrt {1-\left({\frac {v}{c}}\right)^{2}}}$
となります。2点重要なことがあって、①dτ=ds/cとも書ける（式変形なんかで結構つかう。こう書くとdτも基準系の取り方に依らないことが分かるだろう）　②dτはdtよりも小さい、すなわち「動いている時計は止まっている時計より遅く進む」
　特に2つ目の結果について誤解が生じやすいような気がするので補足します（僕も学び始めの時はこの勘違いをしていた）。系Sから見ると系S'に固定された時計は遅れていますが、逆に系S'から系Sに固定されている時計を見るとどうなるでしょうか。普通に考えたら遅れいているの逆で「早まっている」と答えるのが正し気がしますが、実はこれは間違いです。系S'から系Sの時計を見ると動いているのはむしろ系Sの時計であり、そのため系Sの時計の方が遅れて見ええます（そもそも基準系の取り方によって時間の進み方の相対的な関係が変わってしまったら相対性原理に反してしまうでしょう）。
　これらのことは矛盾をきたしてはいないでしょうか？そのことが本書9p.から10p.にかけて議論されています。（ここからはまだ執筆中）
　ところで、この章で初めて登場して、今後も当たり前の言葉として登場する「トラジェクトリー」という言葉ですが、「軌跡」という意味です。普通に翻訳できる言葉なのですが、なぜわざわざカタカナにしているのでしょうか…？

4.ローレンツ変換

　さて、いよいよ慣性基準系の間での変換規則を求めてみましょう。どのようにして決めるかというと、世界間隔を不変に保つようにして決めます。そのような変換は回転に似たような変換になります（実際回転は世界間隔ではなく距離を不変に保つ変換です）。そこでxt平面の"回転"は
$x=x'\cosh \psi +ct'\sinh \psi$
$ct=x'\sinh \psi +ct'\cosh \psi$
と書かれます。納得いかない人はxy平面の回転が
$x=x'\cos \theta +y'\cos \theta$
$y=y'\cos \theta +y'\cos \theta$
で表されることを考えてもらえればわかりやすいと思います。
　もうすこし具体的に考えましょう。x,tを系Kの座標、x',t'を系K'の座標とし、系Kから見た系K'の空間座標の原点を考えます。このとき、x'=0であるので（空間座標の原点を考えているのでt'=0ではない）
$x=ct'\sinh \psi$
$ct=ct'\cosh \psi$
これら2式の比をとると、左辺はx/ct、系K'の系Kに対する相対速度をVとするとV/cとなります（書き忘れましたがVの方向にx軸をとります）。一方で右辺はtanhψになります。これからcoshψとsinhψを計算することで系K'と系Kの座標変数の変換が得られます。
$x={\frac {x'+{\frac {V}{c}}ct'}{\sqrt {1-\left({\frac {V^{2}}{c^{2}}}\right)}}}$
$ct={\frac {ct'+{\frac {V}{c}}x}{\sqrt {1-\left({\frac {V^{2}}{c^{2}}}\right)}}}$
こうして得られた変換をローレンツ変換と言います（この式は上の式と食い違うように思えますが、それは上の式を作るときには系K'の空間の原点に式注目していなかったからです）。
　この変換の逆変換を得るにはVを(-V)に置き換えればいいです。系Kから見て系K'が速度Vで動いているとき、系K'から見ると系Kは速度(-V)で動いていると考えられるからです（追記：よく考えたらいきなりこのように考えるのは少し危険なのかもしれません。まだ得体のしれない空間や変換について考えているのにいきなりこのような推論をしてしまうのは少し怖いです。素直にローレンツ変換をx'とct'について解いた方が無難でしょう。そのうえで「なんだ、要はVを(-V)に置き換えたものじゃないか」と納得するのは自由ですが）。
　このようにこの本では「世界間隔を不変に保つ変換」としてローレンツ変換を定義しています。しかし、ほかの本をあたってみるとこの定義を用いている本はあまりなく、むしろローレンツ変換を物理的な要請から導き、その上で世界間隔が不変であることをその帰結としているものが多いです。その際の物理的な要請というのをここに紹介しておきます。
・光速度が不変
・逆変換ができる
・変換が線型である（「逆変換ができる」に含まれているという考え方もできる）
この辺のリンクも参考にするとよいと思います。
「EMANの物理学」より
yとzが変換を受けない理由についてもきちんと触れています。本稿はあくまでも輪読のレジュメであるためその話をするのは本来の趣旨と外れると考えたためここでは議論しませんでしたが、そこが気になった方がいらっしゃったらここを見てみるとよいと思います。
「FNの高校物理」より
数式をごちゃごちゃいじくるのが物理っぽくなくて気に入らない、という方はこちらの方があっているかもしれません。かなり違ったアプローチからローレンツ変換を導いています。

　この後は、動いている物体は長さが縮んで見えるという、いわゆる「ローレンツ短縮」の話が出ています。これは、物体の両端を同時に観測しているから起こる現象ですね。体積についても、動いている方向のみに短縮が起きるので、長さと同じだけの比率で変化します（すべての方向に短縮が起きるわけではないので「相似比の3乗」のようにはなりません）。電荷密度などを議論するときにもこの考え方を使うので、頭の片隅に入れておくとよいでしょう。

5.速度の変換

　前節では二つの慣性基準系の座標変数がどう変わるかという話をしました。この節では、二つの慣性基準系での速度がどう変換されるかという話をします。前節で得られたローレンツ変換を微小な変位と時間に置き換えて比をとれば速度の変換則が得られます。また、この本には載っていませんがtanhの加法定理
$\tanh(\psi +\phi )={\frac {\tanh \psi +\tanh \phi }{1+\tanh \psi \tan \phi }}$
とx方向の速度の変換則
${\frac {v}{c}}={\frac {{\frac {v'}{c}}+{\frac {V}{c}}}{1+{\frac {v'}{c}}{\frac {V}{c}}}}$
が似ていることも示唆的ですね。ψやφが"回転角"みたいなものに対応するということが分かればこれも納得の結果ではないでしょうか。

　あとは座標系を変えたときに斜めに動いているとき、その方向がどの程度変わるのかという話が出てきています。ここまで細かく書いてある本もなかなかないですね。

6.4元ベクトル

　数学の読み物というのは、なかなか読むのが難しいですよね。いろいろな理由はあると思うのですが、ある程度知識を持っているうえでも読むのが難しいのは、流儀の違いがあるからではないかなと思っています。流儀が違って出発点が異なると、いろいろ論理をこねくり回して出てきた結果が「え、当たり前じゃん」ってなってしまうことがあります。そこでこの章ではほかの本の流儀と区別して「どのような出発点からスタートしているのか」「どのようなものを結果として扱っているのか」を明確にしたいと思います。

　今後相対論を記述するのに使う「テンソル」の導入にあたる節です。ピンとこないことも多いですが、「まぁ、確かに成り立つなぁ…」くらいの理解でとりあえずはいいのかなと思います。
　まずは「4元ベクトル」というものから。この本ではローレンツ変換に従うようなベクトルのことを4元ベクトルと呼んでいます。つまり
$A^{1}={\frac {A^{1'}+{\frac {V}{c}}A^{0'}}{\sqrt {1-\left({\frac {V^{2}}{c^{2}}}\right)}}}$
$A^{0}={\frac {A^{0'}+{\frac {V}{c}}A^{1'}}{\sqrt {1-\left({\frac {V^{2}}{c^{2}}}\right)}}}$
が成り立つようなベクトルを4元ベクトルといい、A^μのように表記します。ベクトルの成分を添え字μで書きますが、訳あって上付きの添え字で書いています。理由は後でわかります。上付きの添え字で書かれるベクトルの成分を「反変成分」といいます。
　「反変」に対する概念として「共変」というのがあります。これはこの本では
$A_{0}=A^{0},A_{i}=-A^{i}(i=1,2,3)$
で定義されています。これは4元ベクトルの大きさの2乗を
$\left(A^{0}\right)^{2}-\left(A^{1}\right)^{2}-\left(A^{2}\right)^{2}-\left(A^{3}\right)^{2}$
で定義する（この定義は世界間隔の定義から自然）ときにこれを
$A^{0}A_{0}+A^{1}A_{1}+A^{2}A_{2}+A^{3}A_{3}$
と書くことができるようにするためです。共変成分を反変成分と区別するため下付きの添え字で書きます。ところで、共変成分の変換規則に関しては、ローレンツ変換に代入してみると得られて、
$A_{1}={\frac {A_{1'}-{\frac {V}{c}}A_{0'}}{\sqrt {1-\left({\frac {V^{2}}{c^{2}}}\right)}}}$
$A_{0}={\frac {A_{0'}-{\frac {V}{c}}A_{1'}}{\sqrt {1-\left({\frac {V^{2}}{c^{2}}}\right)}}}$
となり、ちょうど逆ローレンツ変換になります。
また、添え字の上げ下げは「計量テンソル」と呼ばれる行列を作用させることができるということもわかります。

$g_{\mu \nu }={\begin{pmatrix}1&0&0&0\\0&-1&0&0\\0&0&-1&0\\0&0&0&-1\end{pmatrix}}$

具体的に次のように計算します。
${\begin{aligned}A_{\mu }&=g_{\mu 0}A^{0}+g_{\mu 1}A^{1}+g_{\mu 2}A^{2}+g_{\mu 3}A^{3}\\&=g_{\mu \nu }A^{\nu }\end{aligned}}$
　この計算例を見てわかると思いますが、表記法として「共通の添え字は和をとっているものとして解釈する」というルールがあります。このルールは「縮約」と呼ばれていて、今後頻繁に出てきますので慣れておきましょう。
　ここまでで導入した記号で、試しに微小な世界間隔を書いてみましょう。
${\begin{aligned}ds^{2}&=dx^{0}dx_{0}+dx^{1}dx_{1}+dx^{2}dx_{2}+dx^{3}dx_{3}\\&=dx^{\mu }dx_{\mu }\\&=g_{\mu \nu }dx^{\mu }dx^{\nu }\end{aligned}}$
こう見てみると、計量テンソルは実は微小世界間隔（線素、と言ったりもします）の係数の情報を格納しているとも言えます。実際本によってはこのように定義しているものもありますので注意です。このような定義の仕方は、のちに違う微少世界間隔の表式があることをにおわせていますが、事実その通りです。と言っても、座標変換によって（極座標や円筒座標）表式が変わっているものも含みますが。この定義に則っていく場合は「共変成分は反変成分にある行列を作用させることで得られ、これを計量テンソルという」という主張の仕方より「反変成分に計量テンソルを作用させるとあるベクトルが得られるが、この成分のことを共変成分という」という主張の方が自然に聞こえるでしょう。

　さて、少し脱線しましたが話をもとに戻します。今のところはローレンツ変換に従うような座標変数を反変成分と呼び、それに計量テンソルをかけたものを共変成分と呼ぶのでした。
　しれっと「計量テンソル」という言葉に「テンソル」という聞きなじみのない言葉を使っていますが、次はこれについて説明します。今のところ、ローレンツ変換に従う反変成分と、逆ローレンツ変換に従う共変成分というものがあるとわかっています。「テンソル」はこのような四元ベクトルの一般化です。ちょうど行列がベクトルの一般化であるのに似ています。ただし、行列は数字を2次元的に並べたものであるのに対して、テンソルは何次元で並べても構いません。n次元であれば当然n個の添え字が付きます。また、四元ベクトルの一般化ですので、次のような性質を持ちます。
$T_{\quad \quad \quad \quad \nu _{1'},\nu _{2'},\dots ,\nu _{n'}}^{\mu _{1'},\mu _{2'},\dots ,\mu _{m'}}=\Lambda _{\alpha _{1}}^{\mu _{1'}}\dots \Lambda _{\alpha _{m}}^{\mu _{m'}}\left(\Lambda ^{-1}\right)_{\nu _{1'}}^{\beta _{1'}}\dots \left(\Lambda ^{-1}\right)_{\nu _{n'}}^{\beta _{n}}T_{\quad \quad \quad \quad \beta _{1},\beta _{2},\dots ,\beta _{n}}^{\alpha _{1},\alpha _{2},\dots ,\alpha _{m}}$
ここでいきなり出てきたΛはローレンツ変換を表す行列で、次のように定義します。
$\Lambda _{\nu }^{\mu }={\begin{pmatrix}\gamma &-\beta \gamma &0&0\\-\beta \gamma &\gamma &0&0\\0&0&1&1\\0&0&0&1\end{pmatrix}}$
ただし
$\beta ={\frac {V}{c}},\gamma ={\frac {1}{\sqrt {1-\beta ^{2}}}}$
とする。この文字の置き方は有名なので知っておくとよいでしょう。この行列の逆行列は
$\Lambda _{\nu }^{\mu }={\begin{pmatrix}\gamma &\beta \gamma &0&0\\\beta \gamma &\gamma &0&0\\0&0&1&1\\0&0&0&1\end{pmatrix}}$
になり、ちょうど逆ローレンツ変換を表す行列になっています。一般相対論を扱う頃になると座標変換がローレンツ変換だけではなくなるので、あえて変換を表す行列を用いて表記して、一般的な感じにしています。
　さて、テンソルに関してはこんな感じです。まだまだピンと来ないかもしれませんが、実際に使っていくうちに何となくわかってくるというのが物理学での数学ですので、ある程度のところで妥協しておきましょう。
　つぎは擬テンソルについてです。（現時点ではまだ自分自身の数学の能力がそこまでないので執筆中）

7.4次元的な速度

とりあえず演習問題の解答だけでも載せておきます。
第7節の演習問題
図も載せておきましょう（本来は文章の方に載せたかったが、texで画像がうまく扱えなかった）。赤い線がNewton力学の結果、青い線が相対論の結果です。wt<<cのときに相対論の結果がNewton力学の結果にとても似ていることが分かるかと思います。

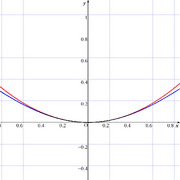
加速度小さめ

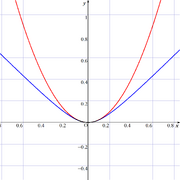
加速度大き目

8.質問コーナー

本稿をここまで読んでいただいて疑問に思ったこと、レジュメとして改善できるようなことなどがあれば（もちろん直接連絡していただいても構わないのですが）ここに書いていただけると助かります。どなたもご自由にお書きください。